Detect Duplicate Subtrees in a Binary Tree
Often in our life we study Data Structures and Algorithms, it can be for a course, interview or just for fun. I personally like to solve interview questions related to trees. I came across a google interview question on careercup.com “Find if a given binary tree has duplicate subtrees”
In this post I will show you how to detect duplicate subtrees in a binary tree.
Prior Knowledge Required
Binary Tree and Python
Background
To check for duplicate subtree tree we first need to uniquely identify each subtrees. A binary tree can be constructed uniquely from a given inorder and postorder traversal reference. With this theory we can represent each subtrees to a unique inorder and postorder traversal pair. Then create a list of inorder and postorder traversals of all subtrees and check if there exist pair that repeats in the list.
Approach
Traditional tree traversals breaks the tree into left subtree and right subtree.
This is done until tree.left and tree.right is not none. The following code
snippet shows inorder traversal.
def print_inorder(tree):
# Left, Root, Right
if tree.left is not None:
print_inorder(tree.left)
print tree.root
if tree.right is not None:
print_inorder(tree.right)As we know that such type of traversal is dividing tree in left and right subtree. we can use the similar approach to divide tree into subtrees and create a list of inorder traversal of this subtrees.
Bellow is modified inorder traversal code snippet.
def get_inorder_subtrees(tree):
global inordersubtree
if (tree.left is None) and (tree.right is None):
return tree.root
temp = ""
if tree.left is not None:
temp = get_inorder_subtrees(tree.left)
temp = temp + tree.root # Left, Root, Right
if tree.right is not None:
temp = temp + get_inorder_subtrees(tree.right)
inordersubtree.append(temp)
return tempLets consider a example. Bellow image shows a tree with duplicate subtree.
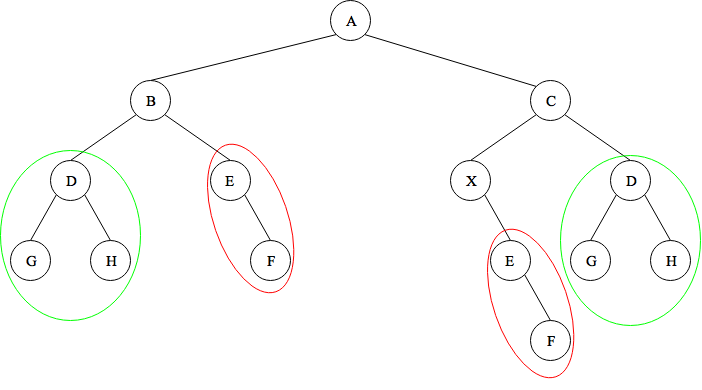
In the above case our modified inorder method get_inorder_subtrees() will
recursively divide the binary tree and save inorder traversal of each subtree
in inordersubtree which is a global list. inordersubtree will contain
['GDH', 'EF', 'GDHBEF', 'EF', 'XEF', 'GDH', 'XEFCGDH', 'GDHBEFAXEFCGDH'] after
traversing the tree.
Similarly we modify postorder traversal.
def get_postorder_subtrees(tree):
global postordersubtree
if (tree.left is None) and (tree.right is None):
return tree.root
temp = ""
if tree.left is not None:
temp = get_postorder_subtrees(tree.left)
if tree.right is not None:
temp = temp + get_postorder_subtrees(tree.right)
temp = temp + tree.root # Left, Right, Root
postordersubtree.append(temp)
return tempget_postorder_subtrees() will also save the postorder traversal in a global
list postordersubtree. postordersubtree will contain
['GHD', 'FE', 'GHDFEB', 'FE', 'FEX', 'GHD', 'FEXGHDC', 'GHDFEBFEXGHDCA'] after
traversing the tree.
Further we create one to one pair of inorder and postorder traversals and check if they are repeating.
for inorder, postorder in zip(inordersubtree, postordersubtree):
if inorder + "-" + postorder in dic:
print "Duplicate Subtrees present"
else:
dic[inorder + "-" + postorder] = "Tree"
print "Binary tree has all unique subtrees"Analysis
Now lets take a look at time and space complexity of this algorithm.
As we know that each node is visited once by this recursion. Hence time
complexity for traversing tree is O(n). We are traversing the tree two times
firstly for inorder and secondly for postorder which will increase time
complexity to O(2n). Further we are comparing pairs of inorder and postorder
of each subtree. let us consider worst case where all nodes only has left
child or all nodes has only right child then in this case time complexity will
increase by O(n). Hence total complexity will be
Tree traversal(O(2n)) + comparing pairs(O(n)). Adding all this complexity we
get O(3n). Since n is the dominating factor and 3 is constant,the constant
can be eliminated. Finally worst-case runtime complexity of above algorithm
is O(n).
Above algorithm is implemented in recursion hence a stack will be used. Recursion
is called on each node, so stack required will be 0(n). Further we are using
a list to store inorder and postorder traversals of all the subtrees. This will
require 0(2(n-1)) space. So total space complexity for this algorithm is
O(n + 2(n-1)) which is approximately O(3n). As we know n is the dominating
factor and 3 is constant. Final worst-case space complexity of above algorithm
is O(n).
Time Complexity: O(n)
Space Complexity: O(n)
Conclusion
There are many such interview questions which I suggest you to have a look at careercup.com. Following gist contains a detailed implementation of above algorithm.
If you have any issues or comments feel free to open an issue at github repo.